2. linear function (y = a x + b)
일차함수 y = a x + b
slope-intercept
form : y = ax + b
"y 절편을 찍은 다음,
기울기 그리기 방법대로 하면 되요"
" plot y-intercept first,
and rise over run "
일차함수의 그래프는, 일차 비례식을 좌표평면에 나타내는 가장 기초적인 내용부터, 중학과정에서는 포물선과 직선 그리고 고등과정에서는 다항함수의 곡선과 직선의 관계까지 다양하게 응용되는 단원입니다.
문과 고등학생 중에는 직선의 그래프도 제대로 못 그려서 쩔쩔매는 모습을 자주 봅니다. 수학실력의 차이는, 함수와 그래프에서 비롯된다고 할 정도로 중요하니, 기초부터 확실하게 다져 두기 바랍니다.
다시 강조하지만, 문과라 하더라도 고등과정의 다항함수의 미적분까지 중고등 수학 전반에서 활용되는 매우 중요한 개념입니다.
♧ ♧ ♧ ♧ ♧ ♧
스마트폰에서 수학 수식을 보시려면, 왼쪽 버튼을 누른 후
[데스크톱 보기] 를 설정하세요.
You can read
math equations
by selecting
[desktop view] on the mobile
♧ ♧ ♧ ♧ ♧ ♧
y = 2x 의 그래프는 기울기가 2 이고 원점을 지나는 직선이라고 배웠던 것을 잘 기억하고 있겠지요? 이번에는 y = 2x + 1 의 그래프를 공부해 보도록 합시다.
We've
learned that the graph of y = 2x is a straight line. It passes
through the origin (0, 0) and its slope is 2. This time, we're going to study the graph of y = 2x + 1.
지난 번과 같이, x 값에 따라 정해지는, y 값들의 순서쌍의 일부를 표로 나타내 볼까요?
Let's
make the table of ordered pairs of (x, y) that satisfy y = 2x
+ 1.
x
|
– 3
|
– 2
|
– 1
|
0
|
1
|
2
|
3
|
y
|
–6+1
|
–4+1
|
–2+1
|
0+1
|
2+1
|
4+1
|
6+1
|
위에서 구한 y = 2x + 1 의 순서쌍인 … (–3, –5), (–2, –3), … , (3, 7) … 들을 좌표평면에 나타내면, 아래 그림에서 보는 것과 같이 빨간색 직선 위의 점들로 표시됩니다.
If we plot (x, y) pairs such as … (–3, –5), (–2, –3), … , (3, 7) … on the coordinate plane, then these pairs will
represent the points on a red straight line as shown below.
따라서, y = 2x + 1을 만족하는, 무수히 많은 (x,
y) 순서쌍들을 모두 표시하면 아래 그림의 빨색 직선이 됩니다. 지난 번에 배웠던 y = 2x 의 그래프와 평행이지요?
Therefore, infinite solution pairs of y = 2x + 1 on the coordinate
plane, they will represent a red straight line as shown below. Can you see that y
= 2x + 1, a red line, is parallel to y = 2x, a blue line
passing through the origin?
다시 살펴보면, 함수식 y = 2x
+ 1 의 y 값들은, y = 2x일 때의 y 값들 보다 1 만큼 크니까, 위 그림에서 파란색으로 표시된 y = 2 x 라는 직선 위의 점들 보다, 모두 1 칸씩 위에 찍히게 됩니다.
It means that we
can draw y = 2x + 1 graph, by moving all points on y = 2x
line up by one unit because y values in solution pairs of y = 2x
+ 1 are always one unit larger than those of y = 2x.
즉, 빨간색의 직선 y = 2x
+ 1 은 y = 2x 를 위로 1 만큼 평행이동시킨 결과가 됩니다.
In other words,
we can sketch y = 2x + 1 line as a parallel translation by +1
along the y-axis.
이제, 공부한 것을 문자를 써서 정리해 볼까요?
Now, we can summarize
what we have learned as follow :
일차함수 y = ax + b 의 그래프는, 원점을 지나는 직선 y = ax 의 그래프를 평행이동시키면 됩니다.
We can draw y = ax + b line graph as a parallel translation of y = ax.
(1) b가 양수 (+) 일 때는, 위로 b 만큼 평행이동
moves up by ' b ' if b > 0
(2) b가 음수 (–) 일 때는, 아래로 b 만큼 평행이동
moves down by ' b ' if b < 0
예를 들어, y = ax +
3 의 그래프는 원점을 지나는 직선 y = ax 를 위로 3 만큼 평행이동시키면 된다는 원리를 알아냈으니까, 쉽고 간단하게 그려낼 수 있는 방법에 대해서 조금 더 공부하도록 할까요?
Having learned
that y = ax + 3 line is a
parallel translation of y = ax + 3 by moving up 3 units, let's
find out more convenient and easier way to draw this line.
직선 y = ax 를 그린 다음, 다시 위로 3 만큼 평행 이동한 y = ax + 3 의 그래프를 그리는 방법도 나쁘지는 않지만, 2 개의 직선을 그려 내야 한다는 점이 조금 불편할 수도 있겠지요?
Drawing the
parallel line is not a bad idea, but we'll have to draw two lines altogether.
따라서, 더 좋은 방법은, 머리 속에서 평행 이동하는 과정을 이미지로 미리 떠올려 본 다음에,
If we're just able to imagine the process of parallel translation, a better way to draw is :
(1) 평행 이동이 완료된 후에, y 축과 만나는 점인 y 절편 (0, 3) 을 y 축 위에 찍습니다.
First of all, plot
y-intercept (0, 3) on y-axis.
(2) 평행한 직선의 기울기는 똑같으니까, 앞에서 배운 [기울기 그리기 방법] 대로 새로운 점을 찾으면 되겠지요?
Two parallel lines have the same slope and therefore, find the other
point using [rise over run] method.
(3) y 절편 (0, 3) 에서 출발해서, [(분모인) 오른쪽으로 몇 칸] 움직일 때, [(분자인) 위 또는 아래로 몇 칸] 이동하는 방법으로 새로운 점을 표시합니다.
Starting from y-intercept (0, 3), move along the path
of [rise over run] to find new point.
(4) y 절편과 새로 찾아낸 두 점을 연결하면 직선의 그래프가 완성됩니다.
Connect the new
point and the y-intercept (0, 3),
then this straight line will be the unique solution.
두 점을 연결하는 직선은 오직 하나이니까, 여러 번 덧칠하지 말고 가급적 한 번에 그려 내면 됩니다. 쉽고 빠르게 정확한 직선을 그려내기 위해서는 부단한 연습을 해두기 바랍니다.
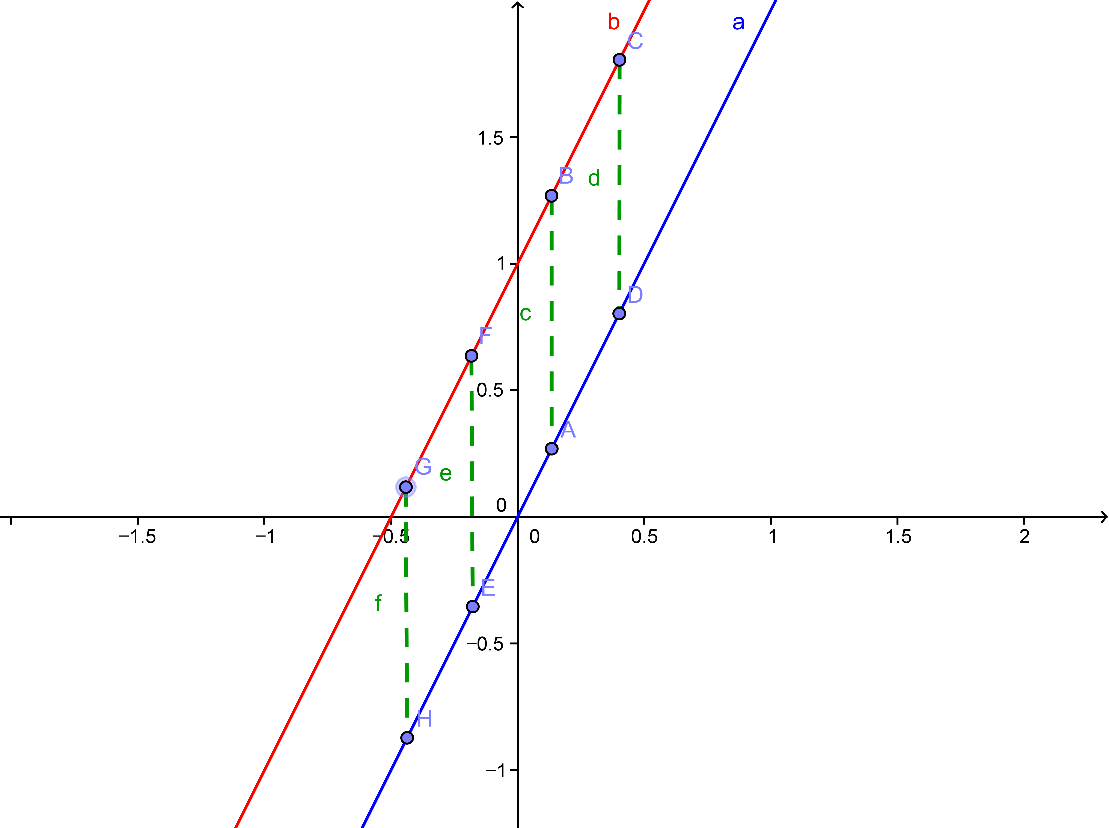
실제로 직선 y = \(\frac{2}{3}\)x + 2
를 같이 그려 보도록 할까요?
As an example, let's
sketch the graph of y = \(\frac{2}{3}\)x + 2.
(1) 제일 먼저, y 절편인 점 (0, 2) 를 y 축 위에 찍습니다.
First of all, plot
y-intercept (0, 2) on y-axis.
(2) y 절편을 찍은 점에서, 기울기를 \(\frac{2}{3}
= \frac{{ + 2}}{{{\rm{ }} + 3{\rm{ }}}}\) 로 해석하여, [(분모인) 오른쪽으로 3 칸] 움직일 때, [(분자인) 위로 2 칸] 이동한 새로운 점 (3, 4) 를 찾아냅니다.
Interpret the slope \(\frac{2}{3} =
\frac{{ + 2}}{{{\rm{ }} + 3{\rm{ }}}}\) as 'rise 2 over run 3'. Move 3 units to
the right and 2 units up from the point (0, 2). Then you will find a new point (3, 4).
(3) y 절편 (0, 2) 와 아래 그림에서 초록색 점선으로 표시된 방법으로 찾아낸 새로운 점 (3, 4) 를 연결하는 직선을, 여러 번 덧칠하지 말고, 가급적 한 번에 그리면 됩니다.
Connect the straight
line that passes through (0, 2) and (3, 4) as shown below :
어느 정도 익숙해진 다음에는, 추가로 배수가 되는 점들 즉, [오른쪽으로 6칸] 갈 때, [위로 4칸] 등을, 또는 반대로 음수 (–) 를 곱해서, [왼쪽으로 6칸] 갈 때, [아래로 4칸] 등을 활용하면, 보다 쉽고 정확하게 그려낼 수 있습니다.
If you feel comfortable in sketching,
after hard practices, then you draw more accurately by using ± multiples of
slope, such as \(\frac{{{\rm{ }} + 6{\rm{ }}}}{{ + 9}}\) or even \(\frac{{{\rm{
}} - 4{\rm{ }}}}{{ - 6}}\).
다시 한번 강조하지만, 분모를 자연수 (+) 로 하는 기약분수로 고치는 이유는, 왼쪽이 아니라 오른쪽을 표준으로 하기 위해서 입니다. 직선의 그래프에 완전히 익숙해 지기전까지는, 항상 [(분모인) 오른쪽으로 몇 칸] 움직일 때, [(분자인) 위 또는 아래로 몇 칸] 간다고 해석해서 그리기 바랍니다.
반드시 이렇게 해야만 하는 것은 아니지만, 기초가 부족한 학생은 처음부터 이 방법으로 숙달을 해 놓으면, 쉽고 빠르게 직선의 그래프를 그릴 수 있으니, 강력하게 추천합니다.
기울기와 y 절편에 양수 (+) 와 음수 (–) 의 여러가지 기약분수의 숫자를 대입해 보면서, 스스로 그래프를 그리는 연습을 충분하게 해두기 바랍니다.
I'd like to
recommend you to practice hard, by replacing the slope or y-intercept
with different fractions or negative values.

Comments
Post a Comment