3. number of elements in a set
집합 원소의 개수
number of elements in a set
"중복된 공통부분은 빼주어야지요"
" subtract common elements
that were counted twice "
집합 원소의 개수는 중 2 와 고 2 의 [경우의 수와 확률] 단원 및 고 1 의 [집합과 명제] 단원에서, 자주 등장하는 합집합과 교집합의 혼합된 개념입니다.
특히, 심화수준의 문제들에서는, 전체의 경우의 수에서 특정조건을 만족하지 않는 반대의 경우를 빼주는, 여집합의 개념과 함께 해결해야 하는 복잡한 유형이 출제됩니다.
기본개념과 공식 정도는 암기해 두어야, 빠른 시간 내에 쉽게 문제를 해결할 수 있습니다.
♧ ♧ ♧ ♧ ♧ ♧
스마트폰에서 수학 수식을 보시려면, 왼쪽 버튼을 누른 후
[데스크톱 보기] 를 설정하세요.
You can read
math equations
by selecting
[desktop view] on the mobile
앞에서, 집합A = {a, b, c} 의 원소의 개수를n (A) = 3 으로 표현한다고 했습니다. 그러면 집합 C = {b, c, e, f} 라 할 때, n (A∪C) 는 어떻게 계산할까요?
We've learned earlier that the number of elements in A
= {a, b, c} is denoted by n (A) = 3. Then, what will be the right answer for n (A∪C), if the set C = {b, c, e, f}?
집합 사이의 관계를 시각적으로 아주 잘 보여 주는 벤 다이어그램 (Venn diagram) 을 이용해서 알아 보도록 하지요.
Venn diagram is
very useful to visualize the relationship between different sets, as shown
below.
위 그림에서 보듯이, n(A∪C) 는 단순히 n (A)
+ n (C) 가 아니라, 중복해서 두 번 더해지는, 빨간색으로 표시된 A∩C = {b, c} 만큼을 다시 빼 주어야 합니다.
As we see in
the diagram above, if we simply add the number of elements in A and C,
then the common elements b and c, will be counted twice. Therefore, we have to
subtract n (A∩C).
n (A∪C)
= n (A) + n (C) – n (A∩C)
= 3 + 4 – 2
= 5
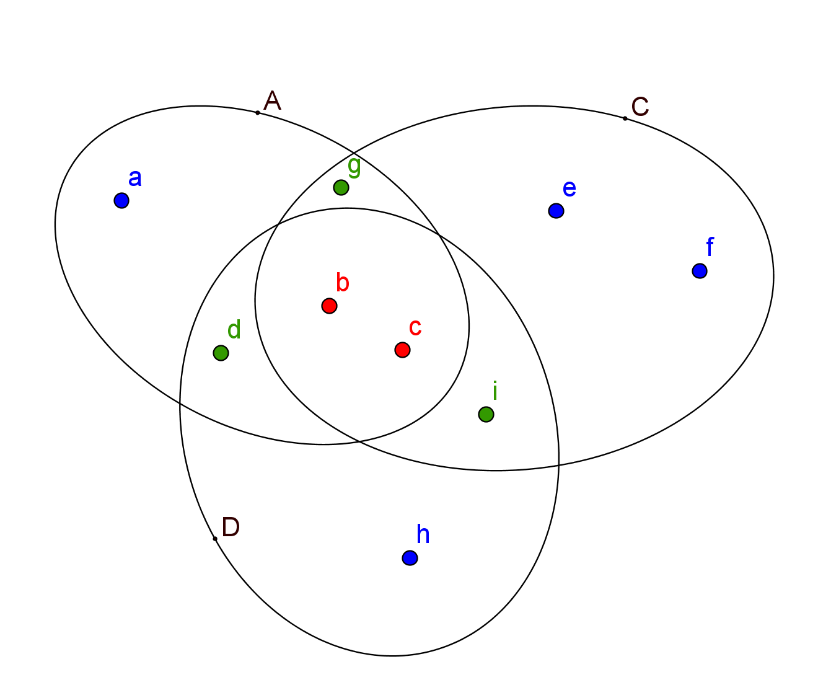
이 원리는 집합의 개수를 늘려나가면 상당히 복잡합니다. 벤 다이어그램에서 집합을 3 개로 확장해서 아래와 같이 그려 보면 되겠죠? 고등수학 과정에서는 3 개까지는 외워 두어야 됩니다.
If we extend the number into three sets, then the
diagram looks quite complex as shown below.
이번에도 위 그림에서 보듯이, n (A∪C∪D) 는 단순하게 n (A) + n (C) +
n (D) 가 아니라,
The above Venn diagram shows us again that n (A∪C∪D) is not simply
the sum of n (A) + n (C) +
n (D).
(1) 중복해서 두 번 더해진, n (A∩C), n (C∩D)
와 n (D∩A)
를 각각 빼 주어야지요.
As we learned before, we have to subtract n (A∩C),
n (C∩D) and n (D∩A)
that were counted twice.
(2) 그런데, 이렇게 3 번을 빼주다 보면, A∩C∩D = {b, c} 는 3 번씩이나 빠졌으니까, 다시 한 번은 도로 더해 주어야 합니다.
On the contrary, the set A∩C∩D = {b, c} has been
subtracted three times and therefore, we have to add this back
again.
n (A∪C∪D)
= n (A) + n (C) + n (D)
– n (A∩C) – n (C∩D) – n (D∩A)
+ n (A∩C∩D)
= 5 + 6 + 5 – 3 – 3 – 3 + 2
= 9
그럼, 공부한 내용을 일반식으로 정리해 볼까요?
Then, let's summarize what we have learned in general form as follows :
Then, let's summarize what we have learned in general form as follows :
n (A∪C∪D)
= n (A) +
n (C) + n (D)
– n (A∩C) – n (C∩D) – n (D∩A)
+ n (A∩C∩D)
이 개념이 어떻게 활용되는지, 예를 한번 볼까요?
100 미만의 자연수 중에서 2 또는 3 또는 5 의 배수인 자연수의 개수를 구하여라.
Find the number
of multiples of 2, 3 and 5, among positive integers less than 100.
(1) 위에서 정리했던 '합집합 원소의 개수' 의 개념을 확실하게 이해했다면, 그대로 공식을 대입하면 되겠지요?
If we have clearly understood the principles summarized
above, then we can simply follow the procedures.
(2) 교집합의 개념을 이용하면, 2 와 3 의 공배수는 6 의 배수이므로 n (2 ∩ 3) = n (6) 이고, 같은 방법으로 아래의 공배수들이 성립합니다.
Common multiples of 2 and 3 are the multiples of 6. Also, we can find the following multiples according to the concept of intersection.
n (2 ∩ 5) = n (10)
n (3 ∩ 5) = n (15)
n (2 ∩ 3 ∩ 5) = n (30)
(3) 따라서, 이를 대입하여 정리하면,
If we simplify the addition of union sets, then
n (2∪3∪5)
= n (2) +
n (3) + n (5)
– n (6) – n (15) – n (10)
+ n (30)
– n (6) – n (15) – n (10)
+ n (30)
= 49 + 33 +19 – 16 – 6
– 9 + 3
= 73

Comments
Post a Comment